Gerak lurus
Gerak lurus adalah gerak suatu obyek yang lintasannya berupa garis lurus. Dapat pula jenis gerak ini disebut sebagai suatu translasi beraturan. Pada rentang waktu yang sama terjadi perpindahan yang besarnya sama.
Gerak lurus beraturan
Gerak lurus beraturan (GLB) adalah gerak lurus suatu obyek, dimana dalam gerak ini kecepatannya tetap atau tanpa percepatan, sehingga jarak yang ditempuh dalam gerak lurus beraturan adalah kelajuan kali waktu.
dengan arti dan satuan dalam SI:
Gerak lurus berubah beraturan
Gerak lurus berubah beraturan (GLBB) adalah gerak lurus suatu obyek, di mana kecepatannya berubah terhadap waktu akibat adanya percepatan yang tetap. Akibat adanya percepatan rumus jarak yang ditempuh tidak lagi linier melainkan kuadratik.
dengan arti dan satuan dalam SI:
Gerak melingkar
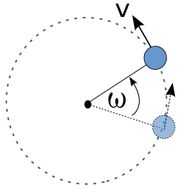
Gerak Melingkar adalah gerak suatu benda yang membentuk lintasan berupa lingkaran mengelilingi suatu titik tetap. Agar suatu benda dapat bergerak melingkar ia membutuhkan adanya gaya yang selalu membelokkan-nya menuju pusat lintasan lingkaran. Gaya ini dinamakan gaya sentripetal. Suatu gerak melingkar beraturan dapat dikatakan sebagai suatu gerak dipercepat beraturan, mengingat perlu adanya suatu percepatan yang besarnya tetap dengan arah yang berubah, yang selalu mengubah arah gerak benda agar menempuh lintasan berbentuk lingkaran [1].
| |
Besaran gerak melingkar
Besaran-besaran yang mendeskripsikan suatu gerak melingkar adalah 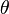 ,
,  dan
dan  atau berturur-turut berarti sudut, kecepatan sudut dan percepatan sudut. Besaran-besaran ini bila dianalogikan dengan gerak linier setara dengan posisi, kecepatan dan percepatan atau dilambangkan berturut-turut dengan
atau berturur-turut berarti sudut, kecepatan sudut dan percepatan sudut. Besaran-besaran ini bila dianalogikan dengan gerak linier setara dengan posisi, kecepatan dan percepatan atau dilambangkan berturut-turut dengan  ,
, 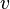 dan
dan  .
.
| Gerak lurus | Gerak melingkar | ||
|---|---|---|---|
| Besaran | Satuan (SI) | Besaran | Satuan (SI) |
poisisi  | m | sudut 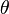 | rad |
kecepatan 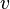 | m/s | kecepatan sudut  | rad/s |
percepatan  | m/s2 | percepatan sudut  | rad/s2 |
| - | - | perioda 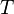 | s |
| - | - | radius  | m |
Turunan dan integral
Seperti halnya kembarannya dalam gerak linier, besaran-besaran gerak melingkar pun memiliki hubungan satu sama lain melalui proses integrasi dan diferensiasi.
Hubungan antar besaran sudut dan tangensial
Antara besaran gerak linier dan melingkar terdapat suatu hubungan melalui  khusus untuk komponen tangensial, yaitu
khusus untuk komponen tangensial, yaitu
Perhatikan bahwa di sini digunakan  yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu
yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu
untuk suatu selang waktu kecil atau sudut yang sempit.
Jenis gerak melingkar
Gerak melingkar dapat dibedakan menjadi dua jenis, atas keseragaman kecepatan sudutnya  , yaitu:
, yaitu:
- gerak melingkar beraturan, dan
- gerak melingkar berubah beraturan.
Gerak melingkar beraturan
Gerak Melingkar Beraturan (GMB) adalah gerak melingkar dengan besar kecepatan sudut  tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial
tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial 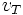 dengan jari-jari lintasan
dengan jari-jari lintasan 
Arah kecepatan linier 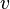 dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial
dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial 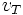 . Tetapnya nilai kecepatan
. Tetapnya nilai kecepatan 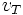 akibat konsekuensi dar tetapnya nilai
akibat konsekuensi dar tetapnya nilai  . Selain itu terdapat pula percepatan radial
. Selain itu terdapat pula percepatan radial  yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
Bila 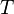 adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran
adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran  , maka dapat pula dituliskan
, maka dapat pula dituliskan
Kinematika gerak melingkar beraturan adalah
dengan  adalah sudut yang dilalui pada suatu saat
adalah sudut yang dilalui pada suatu saat 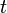 ,
,  adalah sudut mula-mula dan
adalah sudut mula-mula dan  adalah kecepatan sudut (yang tetap nilainya).
adalah kecepatan sudut (yang tetap nilainya).
Gerak melingkar berubah beraturan
Gerak Melingkar Berubah Beraturan (GMBB) adalah gerak melingkar dengan percepatan sudut  tetap. Dalam gerak ini terdapat percepatan tangensial
tetap. Dalam gerak ini terdapat percepatan tangensial  (yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial
(yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial 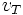 ).
).
Kinematika GMBB adalah
dengan  adalah percepatan sudut yang bernilai tetap dan
adalah percepatan sudut yang bernilai tetap dan  adalah kecepatan sudut mula-mula.
adalah kecepatan sudut mula-mula.
Persamaan parametrik
Gerak melingkar dapat pula dinyatakan dalam persamaan parametrik dengan terlebih dahulu mendefinisikan:
- titik awal gerakan dilakukan
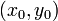
- kecepatan sudut putaran
 (yang berarti suatu GMB)
(yang berarti suatu GMB) - pusat lingkaran

untuk kemudian dibuat persamaannya [2].
Hal pertama yang harus dilakukan adalah menghitung jari-jari lintasan  yang diperoleh melalui:
yang diperoleh melalui:
Setelah diperoleh nilai jari-jari lintasan, persamaan dapat segera dituliskan, yaitu
dengan dua konstanta 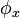 dan
dan 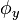 yang masih harus ditentukan nilainya. Dengan persyaratan sebelumnya, yaitu diketahuinya nilai
yang masih harus ditentukan nilainya. Dengan persyaratan sebelumnya, yaitu diketahuinya nilai 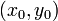 , maka dapat ditentukan nilai
, maka dapat ditentukan nilai 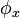 dan
dan 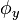 :
:
Perlu diketahui bahwa sebenarnya
karena merupakan sudut awal gerak melingkar.
Hubungan antar besaran linier dan angular
Dengan menggunakan persamaan parametrik, telah dibatasi bahwa besaran linier yang digunakan hanyalah besaran tangensial atau hanya komponen vektor pada arah angular, yang berarti tidak ada komponen vektor dalam arah radial. Dengan batasan ini hubungan antara besaran linier (tangensial) dan angular dapat dengan mudah diturunkan.
Kecepatan tangensial dan kecepatan sudut
Kecepatan linier total dapat diperoleh melalui
dan karena batasan implementasi persamaan parametrik pada gerak melingkar, maka
dengan
diperoleh
sehingga
Percepatan tangensial dan kecepatan sudut
Dengan cara yang sama dengan sebelumnya, percepatan linier total dapat diperoleh melalui
dan karena batasan implementasi persamaan parametrik pada gerak melingkar, maka
dengan
diperoleh
sehingga
Kecepatan sudut tidak tetap
Persamaan parametric dapat pula digunakan apabila gerak melingkar merupakan GMBB, atau bukan lagi GMB dengan terdapatnya kecepatan sudut yang berubah beraturan (atau adanya percepatan sudut). Langkah-langkah yang sama dapat dilakukan, akan tetapi perlu diingat bahwa
dengan  percepatan sudut dan
percepatan sudut dan  kecepatan sudut mula-mula. Penurunan GMBB ini akan menjadi sedikit lebih rumit dibandingkan pada kasus GMB di atas.
kecepatan sudut mula-mula. Penurunan GMBB ini akan menjadi sedikit lebih rumit dibandingkan pada kasus GMB di atas.
Persamaan parametrik di atas, dapat dituliskan dalam bentuk yang lebih umum, yaitu:
di mana  adalah sudut yang dilampaui dalam suatu kurun waktu. Seperti telah disebutkan di atas mengenai hubungan antara
adalah sudut yang dilampaui dalam suatu kurun waktu. Seperti telah disebutkan di atas mengenai hubungan antara 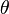 ,
,  dan
dan  melalui proses integrasi dan diferensiasi, maka dalam kasus GMBB hubungan-hubungan tersebut mutlak diperlukan.
melalui proses integrasi dan diferensiasi, maka dalam kasus GMBB hubungan-hubungan tersebut mutlak diperlukan.
Kecepatan sudut
Dengan menggunakan aturan rantai dalam melakukan diferensiasi posisi dari persamaan parametrik terhadap waktu diperoleh
dengan
Dapat dibuktikan bahwa
sama dengan kasus pada GMB.
Percepatan total
Diferensiasi lebih lanjut terhadap waktu pada kecepatan linier memberikan
yang dapat disederhanakan menjadi
Selanjutnya
dengan
yang merupakan percepatan sudut, dan
yang merupakan percepatan sentripetal. Suku sentripetal ini muncul karena benda harus dibelokkan atau kecepatannya harus diubah sehingga bergerak mengikuti lintasan lingkaran.
Gerak berubah beraturan
Gerak melingkar dapat dipandang sebagai gerak berubah beraturan. Bedakan dengan gerak lurus berubah beraturan (GLBB). Konsep kecepatan yang berubah kadang hanya dipahami dalam perubahan besarnya, dalam gerak melingkar beraturan (GMB) besarnya kecepatan adalah tetap, akan tetapi arahnya yang berubah dengan beraturan, bandingkan dengan GLBB yang arahnya tetap akan tetapi besarnya kecepatan yang berubah beraturan.
| Kecepatan | GLBB | GMB |
|---|---|---|
| Besar | berubah | tetap |
| Arah | tetap | berubah |
Gerak jatuh bebas
Gerak jatuh bebas atau GJB adalah salah satu bentuk gerak lurus dalam satu dimensi yang hanya dipengaruhi oleh adanya gaya gravitasi. Variasi dari gerak ini adalah gerak jatuh dipercepat dan gerak peluru.
Rumus umum
Secara umum gerak yang hanya dipengaruhi oleh gaya gravitasi memiliki bentuk:
di mana arti-arti lambang dan satuannya dalam SI adalah
- t adalah waktu (s)
- y adalah posisi pada saat t (m)
- y0 adalah posisi awal (m)
- v0 adalah kecepatan awal (m/s)
- g adalah percepatan gravitasi (m/s2)
Akan tetapi khusus untuk GJB diperlukan syarat tambahan yaitu:
sehingga rumusan di atas menjadi
Analogi gerak jatuh bebas
Apabila gerak jatuh bebas adalah gerak yang hanya dipengaruhi oleh gaya gravitasi, dapat dikemukakan gerak jatuh yang mirip akan tetapi tidak hanya oleh gaya gravitasi, misalnya gerak oleh gaya listrik.
| Gerak oleh gaya gravitasi | Gerak oleh gaya listrik | |
|---|---|---|
| Gaya |  |  |
| Percepatan |  | 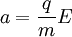 |
| Kecepatan |  |  |
| Posisi |  | 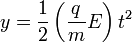 |
Dengan memanfaatkan kedua gaya yang mirip ini percobaan Millikan dilakukan untuk mengukur muatan elektron dengan menggunakan setetes minyak.
Gravitasi
Gravitasi adalah gaya tarik-menarik yang terjadi antara semua partikel yang mempunyai massa di alam semesta. Fisika modern mendeskripsikan gravitasi menggunakan Teori Relativitas Umum dari Einstein, namun hukum gravitasi universal Newton yang lebih sederhana merupakan hampiran yang cukup akurat dalam kebanyakan kasus.
Sebagai contoh, Bumi yang memiliki massa yang sangat besar menghasilkan gaya gravitasi yang sangat besar untuk menarik benda-benda disekitarnya, termasuk makhluk hidup, dan benda benda yang ada di bumi. Gaya gravitasi ini juga menarik benda-benda yang ada diluar angkasa, seperti bulan, meteor, dan benda angkasa laiinnya, termasuk satelite buatan manusia.
Beberapa teori yang belum dapat dibuktikan menyebutkan bahwa gaya gravitasi timbul karena adanya partikel gravitron dalam setiap atom.
Hukum Gravitasi Universal Newton
Hukum gravitasi universal Newton dirumuskan sebagai berikut:
- Setiap massa titik menarik semua massa titik lainnya dengan gaya segaris dengan garis yang menghubungkan kedua titik. Besar gaya tersebut berbanding lurus dengan perkalian kedua massa tersebut dan berbanding terbalik dengan kuadrat jarak antara kedua massa titik tersebut.
- F adalah besar dari gaya gravitasi antara kedua massa titik tersebut
- G adalah konstanta gravitasi
- m1 adalah besar massa titik pertama
- m2 adalah besar massa titik kedua
- r adalah jarak antara kedua massa titik
Dalam sistem Internasional, F diukur dalam newton (N), m1 dan m2 dalam kilograms (kg), r dalam meter (m), dsn konstanta G kira-kira sama dengan 6,67 × 10−11 N m2 kg−2.
Dari persamaan ini dapat diturunkan persamaan untuk menghitung Berat. Berat suatu benda adalah hasil kali massa benda tersebut dengan percepatan gravitasi bumi. Persamaan tersebut dapat dituliskan sebagai berikut: W = mg. W adalah gaya berat benda tersebut, m adalah massa dan g adalah percepatan gravitasi. Percepatan gravitasi ini berbeda-beda dari satu tempat ke tempat lain.
Hukum Gerakan Planet Kepler

Di dalam astronomi, tiga Hukum Gerakan Planet Kepler adalah
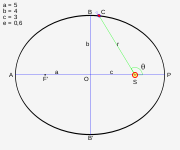
- Setiap planet bergerak dengan lintasan elips, matahari berada di salah satu fokusnya.
- Luas daerah yang disapu pada selang waktu yang sama akan selalu sama.
- Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari matahari.
Ketiga hukum diatas ditemukan oleh ahli matematika and astronomi jerman Johannes Kepler (1571–1630), yang menjelaskan gerakan planet di dalam tata surya. Hukum diatas menjabarkan gerakan dua benda yang saling mengorbit.
Karya Kepler didasari oleh data observasi Tycho Brahe, yang diterbitkannya sebagai 'Rudolphine tables'. Sekitar tahun 1605 Kepler menyimpulkan bahwa data posisi planet hasil observasi Brahe mengikuti rumusan matematika cukup sederhana yang tercantum diatas.
Hukum Kepler mempertanyakan kebenaran astronomi dan fisika warisan zaman Aristoteles dan Ptolemaeus. Ungkapan Kepler bahwa Bumi beredear sekeliling, berbentuk elips dan bukannya epicycle, dan membuktikan bahwa kecepatan gerak planet bervariasi, merubah astronomi dan fisika. Hampir seabad kemudian Isaac Newton mendeduksi Hukum Kepler dari rumusan hukum karyanya, hukum gerak dan hukum gravitasi Newton, dengan menggunakan Euclidean geometry klasik.
Pada era modern, hukum kepler digunakan untuk aproximasi orbit satelit dan benda-benda yang mengorbit matahari. Yang semuanya belum ditemukan pada saat Kepler hidup. (contoh: planet luar dan asteroid) Hukum ini kemudian diaplikasikan untuk semua benda kecil yang mengorbit benda lain yang jauh lebih besar, walaupun beberapa aspek seperti gesekan atmosfer (contoh: gerakan di orbit rendah), atau relativitas (contoh: prosesi preihelion merkurius), dan keberadaan benda lainnya dapat membuat hasil hitungan tidak akurat dalam berbagai keperluan.
Introduksi Tiga Hukum Kepler
Secara Umum
Hukum hukum ini menjabarkan gerakan dua badan yang mengorbit satu sama lainnya. Masa dari kedua badan ini bisa hampir sama, sebagai contoh Charon—Pluto (~1:10), proporsi yang kecil, sebagain contol. Bulan—Bumi(~1:100), atau perbandingan proporsi yang besar, sebagai contoh Merkurius—Matahari (~1:10,000,000).
Dalam semua contoh diatas kedua badan mengorbit mengelilingi satu pusat masa, barycenter, tidak satupun berdiri secara sepenuhnya di atas fokus elips. Namun kedua orbit itu adalah elips dengan satu titik fokus di barycenter. Jika ratio masanya besar, sebagai contoh planet mengelilingi matahari, barycenternya terletak jauh di tengah obyek yang besar, dekat di titik masanya. Di dalam contoh ini, perlu digunakan instrumen presisi canggih untuk mendeteksi pemisahan barycenter dari titik masa benda yang lebih besar. Jadi, hukum Kepler pertama secara akurat menjabarkan orbit sebuah planet mengelilingi matahari.
Karena Kepler menulis hukumnya untuk aplikasi orbit planet dan matahari, dan tidak mengenal generalitas hukumnya, artikel wikini ini hanya akan mendiskusikan hukum diatas sehubingan dengan matahari dan planet-planetnya.
Hukum Pertama
- "Setiap planet bergerak dengan lintasan elips, matahari berada di salah satu fokusnya."
Pada zaman Kepler, klaim diatas adalah radikal. Kepercayaan yang berlaku (terutama yang berbasis teori epicycle) adalah bahwa orbit harus didasari lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.
Meski secara teknis elips yang tidak sama dengan lingkaran, tetapi sebagian besar planet planet mengikuti orbit yang bereksentrisitas rendah, jadi secara kasar bisa dibilang mengaproximasi lingkaran. Jadi, kalau ditilik dari observasi jalan edaran planet, tidak jelas kalau orbit sebuah planet adalah elips. Namun, dari bukti perhitungan Kepler, orbit orbit itu adalah elips, yang juga memeperbolehkan benda-benda angkasa yang jauh dari matahari untuk memiliki orbit elips. Benda-benda angkasa ini tentunya sudah banyak dicatat oleh ahli astronomi, seperti komet dan asteroid. Sebagai contoh Pluto, yang diobservasi pada akhir tahun 1930, terutama terlambat diketemukan karena bentuk orbitnya yang sangat elipse dan kecil ukurannya.
Hukum Kedua
- "Luas daerah yang disapu pada selang waktu yang sama akan selalu sama."
Secara matematis:
dimana 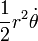 adalah "areal velocity".
adalah "areal velocity".
Hukum Ketiga
Planet yang terletak jauh dari matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepelr ketiga menjabarkan hal tersebut secara kuantitativ.
- "Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari matahari."
Secara matematis:
dimana P adalah period orbit planet dan a adalah axis semimajor orbitnya.
Konstant proporsionalitasnya adalah semua sama untuk planet yang mengedar matahari.
Sejarah
Pada tahun 1601 Kepler berusaha mencocokkan berbagai bentuk kurva geometri pada data-data posisi Planet Mars yang dikumpulkan oleh Tycho Brahe. Hingga tahun 1606, setelah hampir setahun menghabiskan waktunya hanya untuk mencari penyelesaian perbedaan sebesar 8 menit busur (mungkin bagi kebanyakan orang hal ini akan diabaikan), Kepler mendapatkan orbit planet Mars. Menurut Kepler, lintasan berbentuk elips adalah gerakan yang paling sesuai untuk orbit planet yang mengitari matahari, dan pada tahun 1609 dia mempublikasikan Astronomia Nova yang menyatakan dua hukum gerak planet. Hukum ketiga tertulis dalam Harmonices Mundi yang dipublikasikan sepuluh tahun kemudian.

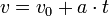
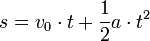

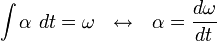
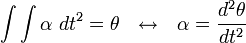

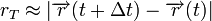
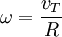







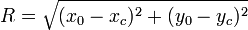




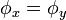





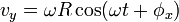
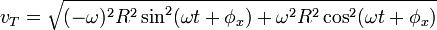

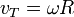



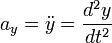
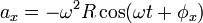








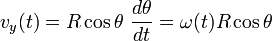






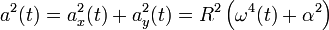






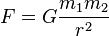

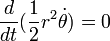
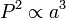

Website download bukunya dimana massssss ??????
BalasHapusNtaps (y)
BalasHapusCasino Finder - Find Casinos Near You (2021)
BalasHapusFind your nearest 사천 출장안마 casino and 제주도 출장안마 find your closest Casino 경산 출장샵 Finder! Use our complete Local Casino Finder to find the BEST & 통영 출장안마 NEWEST 이천 출장마사지 Casinos in Washington, D.C..